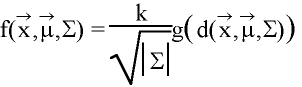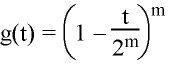Normal Distribution Mapping
UNC Chapel Hill Computer Science Technical Report 97-041
(also available in Adobe Acrobat format)
ABSTRACT
Normal distribution mapping is an extension of traditional texture
mapping methods to normal and shading information. The surface normal
direction and shading for a patch of surface are represented by a statistical
distribution of normal directions. The normal distribution map is a map of
these distributions as they vary over the surface. Normal distribution mapping
admits considerable freedom in the choice of probability density function. We
propose using a distribution based on a 3D Gaussian for this purpose. This
distribution can be easily filtered for map antialiasing and cheaply evaluated
for surface shading.
In the same way that texture mapping provides separation between the
sampling of the surface color and the surface geometry, normal distribution
mapping separates the sampling of the surface normals and surface
geometry. With a normal distribution MIP-map, the normal and shading
information can be appropriately filtered and resampled based on pixel
coverage. These two properties mean that normal distribution mapping can
improve the sampling and filtering of shading information on polygonal
approximations surfaces, either polygonalization of smooth surfaces or coarse
level of detail surfaces.
Since the normal distribution map uses a single representation that
combines properties of bump maps with surface shading information, it also
provides continuous transitions between these domains. In fact, calling it a
"transition" is not accurate since normal distribution mapping uses a single
unified representation for both domains.
CR Categories and Keywords: G.3 Probability and statistics; I.3.3
Picture/Image Generation; I.3.7 Three-Dimensional Graphics and Realism;
Surface Shading; BRDF; texture mapping; bump mapping; multiresolution
analysis
1 INTRODUCTION
One way to think about polygonal representations of smooth surfaces is in
terms of sampling and reconstruction. Each vertex is a sample of the smooth
surface. We reconstruct an approximation to that surface from the vertex
sample locations. The quality of the polygonal approximation depends on the
sampling rate and distribution - how many vertices were used and where they
were placed.
Sometimes we will also use a color and normal at each vertex to reconstruct
the color and shading of the smooth surface. However, the sampling that is
most appropriate for the surface geometry is not necessarily the best choice
for reconstructing the surface color, and the best rate for the color is not
best for the geometry. Texture mapping addresses this problem by divorcing the
sampling of the color from the sampling of the geometry.

a) |

b) |
Figure 1: Color and normal distribution
map textures on a simple object, with filtering on both done using a
MIP-map. a) color and normal distribution map textures on a simple
object. b) same textures at a different MIP-map scale (under-sampled for
this image size). Note how the specular highlight blurs and elongates in
the direction of the ripples. |
While texturing solves the problems of color sampling, we still sample
surface normals at the vertices (see Figure
1). Gouraud shading and Phong shading provide different schemes for
reconstructing the smooth surface shading from the sampled normals. We have
observed in recent work in level of detail and multiresolution surface
approximation, that appropriate sampling for the surface geometry does not
necessarily provide appropriate sampling for the normals either. For example,
simplification envelopes [Cohen96] can guarantee that
the polygonal approximation to a surface is correct to within one pixel. Yet
the surface highlights may change drastically between one level of detail and
the next (see Figure 2). We are aware of work in progress
to incorporate surface normal and curvature information in the simplification
process, but this will result in excess polygons, not necessary to represent
the geometry faithfully. If we can separate the normal sampling from the
geometry sampling, it will be possible to do model simplification based only
on geometric constraints, without introducing extra polygons.
Williams also noticed problems sampling the surface highlights in image
space, which he called highlight aliasing [Williams83]. One form of highlight aliasing occurs
when geometry normals change rapidly with respect to the image sampling
frequency. This is particularly apparent for regular bumps, where the bump
highlights beat against the image samples. The second form of highlight
aliasing occurs on very shiny surfaces when the highlight size is close to the
spacing between image samples. His solution used an illumination MIP-map for
the specular component of the surface illumination, though this solution is
only applicable for non-local lighting.
Some of these sampling problems could be avoided by using a normal map. We
will be referring to a number of different maps on the surface. These are
functions defined over the surface, usually through some texture coordinate
system. For example, a texture map gives a color at every point on the
surface; a normal map gives a normal at every point on the surface; a bump map
gives a perturbation of the normal at every point on the surface. In general,
unless there is another already common term for a map, we will name the map
after the thing being mapped.
While the normal map decouples geometry sampling density from normal
sampling density, it is still necessary to properly filter it to avoid
aliasing. For color textures, pre-filtering techniques are commonly used speed
the filtering process during rendering. For example, MIP-mapping computes a
pyramid of pre-filtered versions [Williams83]. We
can consider creating a hierarchy of maps for any map, and can apply standard
MIP-mapping and signal processing techniques on any map which behaves
linearly.
While normals may be linearly combined and averaged, directly filtering the
normal map does not yield the expected results. Consider the example of sheet
of aluminum foil that has been crumpled then flattened again. When examined
closely, it appears to be a shiny surface with surface normals pointing in
many directions. From a sufficient distance, the wrinkles are no longer
apparent, and it appears to be a single flat surface with a common
normal. However, at this scale the sheet no longer produces a clean reflection
- it appears less shiny. A filtered version of the normal map correctly shows
the new common normal direction, but does not reflect the changes in surface
shading.
The solution is to incorporate information about the distribution of
normals in the closer view into the shading computations in the more distant
view. We need an approximation to the bidirectional reflectance distribution
function (BRDF) of the surface at the distant scale that is derived from a
combination of the BRDF and normals at the close scale.
2 CHANGING SCALES
Cabral et al. produced a BRDF for a distant view of a bump mapped surface
using Monte Carlo ray tracing techniques [Cabral87]. The close view of the bump map was modeled as
a height field, and random rays (modulated by the close scale BRDF) were
traced to produce a histogram representation of the distant scale BRDF for the
entire bump map. This distant BRDF could be fit by an appropriate
approximation function for computation. Westin et al. used similar methods to
produce a milliscale BRDF from surface geometry and microscale BRDF [Westin92].
Both of these produced BRDFs at discrete scales. In a follow-on to the
Cabral et al. work, Becker and Max addressed the transition between
representations at different scales [Becker93]. To
blend between bump mapping and BRDF representations, they blended between the
color produced by each. They also allowed a hierarchy of scales, with Perlin's
technique of band-limiting the frequency of the bumps [Perlin84]. This technique uses a frequency cut-off at
each scale to decompose the bumps into a part to be rendered using the BRDF
and a part to be rendered using bump-mapping.
Fournier eliminated the problem of blending between bump mapping and BRDF
by combining both into an approximation to the BRDF, which varied over the
surface [Fournier92]. He could also handle a
hierarchy of scales using a pyramid of these approximations, similar to a
MIP-map. This is the approach we use for our normal distribution maps.
A common approach to approximating a BRDF is to split it into separate
components for diffuse and specular reflection. The diffuse component can be
represented as simple Lambertian shading. The specular component can be
represented as a probability distribution of normals. This is usually derived
by imagining the surface as composed of millions of perfectly reflective
microfacets, randomly distributed about the average normal direction (see Figure 3). These facets are too small to see, but can
be modeled with geometric optics. For any particular light and view direction,
there is some probability of having facets with the normal direction that
reflects the light to the viewer. This probability can be found by looking
directly at the value of the probability density function, and can be used
directly to determine the percentage of light that reflects from the light to
viewer.
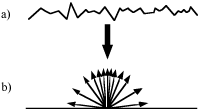 |
Figure 3: Surface
microfacets. a) The surface is assumed to be made of millions of tiny
facets. The facets are used to find a probability distribution of facet
normal directions. b) The surface is rendered as a geometrically flat
surface with the normal distribution used to reproduce the shading effects
of the facets. |
The Blinn [Blinn77] model adds a term for geometric
attenuation (from shadowing and masking occlusion effects). Shadowing, of
course, is when one part of the object blocks the path between the light and
surface. Masking is when part of the object blocks the path between viewer
and surface. Dealing with these effects can be troublesome and expensive.
Many rendering systems do not deal with the shadowing effects (they do deal
with masking since this is the visibility problem). Bump maps, generally do
not account for either shadowing or masking. The best known technique for
dealing with occlusion effects in the context of bump mapping and shading is
the work of Max and Becker [Becker93]. Their
technique could be adapted to our normal distribution maps. We have elected
not to do this in an attempt to keep the computational cost of the method
low. Note also that Ward, while he was addressing a different problem,
achieved good fit to measured BRDFs without any geometric attenuation [Ward92].
So far, we have a BRDF map over the surface. By allowing the BRDF to vary
over the surface, we combine bump mapping and surface shading effects into a
single representation, avoiding problems that occur when transitioning between
these effects when they are modeled separately. We approximate this BRDF map a
normal distribution map, basically approximating each BRDF by a statistical
distribution of surface normal directions. The main choice that remains to be
made is the probability distribution to use. In searching for a distribution,
we are interested in three key properties. First, it should be able to
reproduce a Gaussian-like distribution of normals. Second, it must be cheap to
evaluate during shading. Third, it should be easy to filter for producing a
MIP-map. If possible, we would like the parameters of the distribution to
combine linearly, so standard filtering and MIP-map lookup techniques can be
applied directly.
3 MICROFACETS ON LARGE SECTIONS OF SURFACE
Microfacet shading models are of interest since they also model the
statistical distribution of surface normals, albiet locally. These models
generally assume that the only variation is due to the microfacet
orientations. Otherwise, the surface is flat. This is reasonable for the
context where these models are used. To understand what it means to represent
the normals for a larger section of surface, we use a tool from differential
geometry, the Gauss map [Koenderink90]. Every point on the surface has a unit
normal associated with it. That unit normal can be interepreted as a point on
a unit sphere. Thus, the normals of the surface define a mapping between the
surface and the unit sphere. This mapping is called the Gauss map. When the
mapping is applied to a particular surface, the result is called the Gauss map
of the surface (see Figure 4).
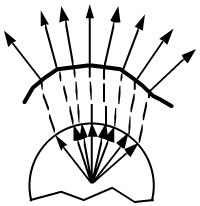 |
Figure 4. 2D example of a Gauss map for a section
of a curve. This is the mapping of the curve onto the unit circle based on
curve normal direction. It is analogous to the 3D Gauss map, which maps a
surface onto the unit sphere. Compare this figure to Figure 3. |
For our purposes, we are not interested in the shape or connectivity of the
Gauss map, but its density. We can model the density of the Gauss map with a
probability density function on the sphere. Each texel in the normal
distribution map models the distribution of normals on the Gauss map for a
section of surface. The texels in a normal distribution MIP-map cover
progressively larger pieces of surface at each MIP-map level.
4 DISTRIBUTIONS ON THE SPHERE
Microfacet models generally use probability distributions over a hemisphere
of the Gauss map, pointing outward from the local surface direction. Even if
we start with these hemispherical distributions, as we combine them at coarser
MIP-map levels, the probability of normals below the "horizon" increases. As a
result, we are interested in probability distributions over the entire Gauss
map. That is to say, probability distributions on a sphere.
Any distribution on the hemisphere can be used on the sphere by using a
zero probability for any normals in the other hemisphere. This is the approach
taken by Fournier, who used distributions based on mixtures of Gaussians,
which he approximated as "Phong Peaks" for cheaper shading [Fournier92]. If we want our density function to
represent the normals on the other side of the sphere we need a different type
of distribution. Also, where Fournier placed more emphasis on the accuracy of
the approximation to the BRDF, we place more emphasis on speed. We want a way
to achieve most of the visual improvement without having to compute mixtures
of up to fifty Gaussians. If possible, we would also like to avoid the hours
non-linear optimization to fit the approximations in the pre-processing
stages.
Microfacet models are created by applying geometric optics to simple
shapes. Blinn used `V' shaped grooves [Blinn77] for
one shading model and spheres for another [Blinn82]. Poulin used parallel cylindrical grooves [Poulin90]. Neyret used this geometric technique to
derive a distribution for use in volume shading that covered the full Gauss
map [Neyret95]. He used a single randomly sized and
oriented ellipsoid to produce his distribution of normals. Neyret's work is
interesting because, when producing an octtree representation of the volume,
parent cells were represented by a single ellipsoid that approximated all of
the ellipsoids in the children cells. This allows basic filtering operations
to always result in an approximation of the same form. We will come back to
this idea later.
The real result of any geometric microfacet model is a distribution of
normals. Other shading models have used distributions without any reference
to geometry, based only on the distribution's ability to approximate the BRDF
[Ward92]. So we may consider other distributions if they
have the right Gaussian character and are easier to compute or filter.
One way to create new distributions is to a way to generalize existing
ones. For example, the `V' shaped microfacet grooves are usually assumed to
have a Gaussian distribution of slopes. The resulting distribution can also be
seen as a projection of a Gaussian onto the hemisphere as follows: define a
Gaussian distribution on a plane and place this plane tangent to the top of
the hemisphere. To find the probability density at a point on the hemisphere,
project from the center of the sphere, through the point, onto the plane (see
Figure 5 a). The value of the Gaussian density
function on the plane defines a density for the point on the sphere.
Mean vector: 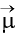
Covariance matrix: 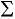
Gaussian density: 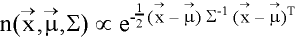
Gaussian projected to hemisphere: ![n([x y]/z, u, S)](hemisphere.gif)
One of the first probability distributions we tried was an extension of
this to the full sphere. Instead of projecting from the center of the sphere,
we tried projecting from the opposite pole (a stereographic projection).
Gaussian projected to full sphere: ![n([x y]/(z+1), u, S)](sphere.gif)
The result is a Gaussian-like distribution, defined over the whole Gauss
map (see Figure 5 b). Unfortunately, this
distribution is quite difficult to combine and filter, and the approximation
we get when we combine a mixture of two distributions into a single one is not
a good one.
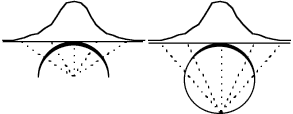 |
Figure 5. Creating a distribution on the sphere
by projection. a) The density function for a Gaussian distribution of
microfacet slopes can also be created by projection from the center of the
sphere. b) A similar density function over the full sphere. |
The final class of distributions we consider are not based on microfacet
models at all. Johnson gives a number of probability distributions on the
circle and sphere [Johnson87]. These distributions
are formed by starting with a distribution in Euclidean 3-space, and using the
conditional probability of the distribution when restricted to the surface of
the sphere. This opens up the possibility of working in Euclidean space, where
distributions tend to be better behaved, instead of on the sphere.
5 DISTRIBUTION INDUCED BY A 3D GAUSSIAN
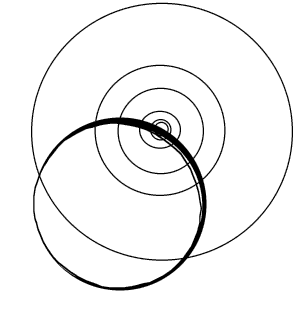 |
Figure 6:2D example of a distribution on a circle
created by restricting a 2D Gaussian to the circle. This can be extended
to create a distribution on a sphere from a 3D Gaussian. |
A requirement for any distribution is that it be able to reproduce the
tight 2D Gaussian-like cluster of normal directions on shiny surfaces. If we
consider possible 3D distributions to produce Gaussian behavior, the first
distribution that comes to mind is the 3D Gaussian. A low-variance Gaussian
centered on the surface of the Gauss map can certainly create a Gaussian-like
cluster of normals on the surface of the Gauss map. The mean of the 3D
Gaussian is the average normal direction for that point on the shiny
surface. The distribution defines a small Gaussian blob in space around that
average normal direction (see Figure 6).
Further, simple 3D Gaussians are easy to combine linearly. The best
Gaussian fit to a mixture of two 3D Gaussians has a mean that is an average of
the means of the two original Gaussians. The variances do not combine
linearly, but the second moments about the origin do [Johnson87].
Distributions: 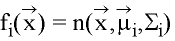
with mean vector 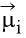 and
covariance matrix
and
covariance matrix 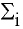
Second central moment: 
Mixture: 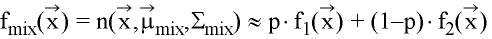
Mean: 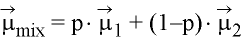
Second central moment: 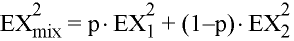
Covariance matrix: 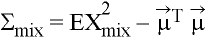
To clarify the mixture of these 3D Gaussians, consider a shiny bump on a
surface. Two nearby locations will both be characterized by low-variance
distributions with slightly different means. Low-variance because the surface
is shiny, differing means because the normal directions on different points on
the bump are different. When we combine an equal mixture of these two
distributions, the new mean is the average of the two original means. This
means that the total average normal direction is the average of the original
two normal directions. The variance increases along the axis between the two
original means, while remaining the same in the other directions. The
variation in original normal directions turns into additional uncertainty in
the distribution of normals.
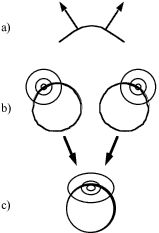 |
Figure 7:Mixture of 2D Gaussians: a) A shiny
bump, sampled at two points, each with a different normal. b) The
concentric circles are contours of the 2D Gaussians on the Gauss map for
each sample point. The thickness of the circles indicates indicates the
actual probability density induced on each Gauss map. c) The two 2D
Gaussians from (b) are combined into a single 2D Gaussian. Note the
increase in variance. |
We can characterize the 3D Gaussian density function with nine numbers, all
of which combine linearly. Three for the mean and six for the matrix of second
moments. We can put these nine numbers into a MIP-map, and filtering will work
as expected. In fact, in our implementation, we treat these nine numbers as
three separate three-color MIP-maps with 16 bits per component. No changes to
either MIP-map creation or access were necessary.
For our previous example of the sheet of aluminum foil, in the close view
we have Gaussian distributions with small variance (corresponding to a shiny
surface), but differing means. In the distant view, all of the Gaussians have
similar means, but a larger variance (corresponding to a duller surface). This
is exactly the behavior we want. Similarly, for grooved surfaces, the variance
will increase more in one direction than the other as the object becomes
smaller, modeling the anisotropic reflection.
6 SHADING USING THE 3D GAUSSIAN
The most time critical computation is not the creation of the normal
distribution MIP-map, but its use during shading. Since the 3D Gaussian-based
normal distribution map behaves linearly, the MIP-map lookup computations are
straightforward. The result is a single 3D Gaussian to be used as the normal
distribution for an image sample. We must compute the normalized halfway
vector between the light and viewer and look this up in the density
function. Ignoring normalization of the density function for the moment, this
just involves plugging the halfway vector into the 3D Gaussian function.
To this point, we have been able to work with the probability distributions
without constructing their density functions. We know the form of the density
function, but it must still be normalized so the total probability over the
entire sphere is one. To do this, we integrate the 3D distribution over the
sphere and divide by the result. Unfortunately, the Gaussian distribution does
not integrate well over the sphere.
We could compute these integrals numerically at every image sample, but
that is far too expensive. Instead, we can do the numerical integration as a
pre-process for each element of the normal distribution MIP-map, producing a
MIP-map of normalization factors. The resulting tri-linear interpolation is
only an approximation to the true normalization factor, but is much cheaper to
compute.
An alternate method is to use the 3D Gaussian for MIP-mapping only, and
approximate the resulting 3D distribution for shading. For example, since the
restriction of a 3D Gaussian to a plane is a 2D Gaussian [Johnson87]. One possible approximation is to choose a
plane tangent to the sphere or one through the mean of the 3D Gaussian, and
project the the distribution on this plane onto the sphere. To summarize, we
approximate the BRDF with a 3D Gaussian for MIP-mapping, then re-approximate
with a projected 2D Gaussian for rendering.
As a final option, we can follow the "traditional" graphics approach and
the 3D Gaussian, but use an un-normalized density function. It is still
necessary to do a partial normalization based on the square root of the
covariance matrix to factor out changes due to the changing variance of the 3D
Gaussian. Surprisingly, this works reasonably well. Since it is, by far,
computationally the least expensive, it was the method used for all the images
shown in this paper.
Even if we ignore the normalization of the density function, the
computation of the Gaussian is still rather expensive, since it involves an
exponential. To make the computation cheaper, we actually use an approximation
to the 3D Gaussian. Johnson discusses the class of elliptically contoured
distributions, which include the Gaussian distribution.
Distance function: 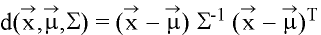
Density function (for a given g(t)): 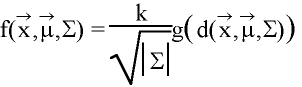
Gaussian distribution: 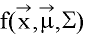 for
for 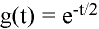
Lyon shows that the Phong and Pearson Type II both do a good job of
approximating a Gaussian [Lyon93]. We choose, as he did,
to use the Pearson Type II distribution for its computational simplicity.
Pearson Type II distribution: 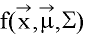 for
for 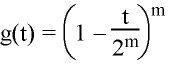
The parameter m is a constant that controls how closely the Pearson Type II
distribution matches the Gaussian (we used eight).
7 CONCLUSIONS AND FUTURE WORK
We have presented a new method for uniformly handling sampling of surface
normals and shading information, and the interaction between the two at
different distances. The method uses a probability distribution of surface
normal directions as an approximation to the BRDF as it varies over the
surface. We propose using a probability distribution based on a 3D Gaussian
for this purpose. The parameters definining this distribution behave linearly,
so they can be easily filtered using standard filtering techniques. An
approximation to this distribution can be used that is fast to evaluate at
shading time, or several progressively more expensive alternatives exist for
normalizing the distribution if it becomes necessary.
Though shadowing and masking effects cannot occur on bump maps, they can
occur if the surface model is more complex. We would like to be able to model
these effects. The likely method for creating these models has been
previously proposed by Becker.
Finally, we would like to explore multi-resolution simplification using
probability density functions based on wavelets which have "nice"
recombination behavior.
8 REFERENCES
[Becker93] Barry Becker and Nelson Max, "Smooth
Transitions between Bump Rendering Algorithms", Proceedings of SIGGRAPH `93
(Anaheim, California, August 1-6, 1993). In Computer Graphics, Annual
Conference Series, 1993, ACM SIGGRAPH, New York, 1993.
[Blinn82] James Blinn, "Light Reflection Functions
for Simulation of Clouds and Dusty Surfaces", Proceedings of SIGGRAPH `82
(Boston, Massachusetts, July 26-30, 1982), In Computer Graphics, v16n3,
ACM SIGGRAPH, New York, 1982.
[Blinn77] James Blinn, "Models of Light Reflection
for Computer Synthesized Pictures", Proceedings of SIGGRAPH `77 (San Jose,
California, July 20-22, 1977), In Computer Graphics, v11n2, ACM
SIGGRAPH, New York, 1977.
[Cabral87] Brian Cabral, Nelson Max and Rebecca
Springmeyer, "Bidirectional Reflection Functions from Surface Bump Maps",
Proceedings of SIGGRAPH `87 (Anaheim, California, July 21-31, 1987), In
Computer Graphics, v21n4, ACM SIGGRAH, New York, 1987
[Cohen96] Jonathan Cohen, Amitabh Varshney, Dinesh
Manocha, Greg Turk, Hans Weber, Pankaj Agarwal, Frederick Brooks and William
Wright, "Simplification Envelopes", Proceedings of SIGGRAPH `96 (New Orleans,
Louisiana, August 4-6, 1996). In Computer Graphics, Annual Conference
Series, 1996, ACM SIGGRAPH, New York, 1996.
[Cook82] Rob Cook and Ken Torrance, "A Reflectance
Model for Computer Graphics", ACM Transactions on Graphics, v1n1,
January 1982, ACM, New York, 1982.
[Fournier92] Alain Fournier, "Filtering Normal
Maps and Creating Multiple Surfaces", Technical Report TR-92-41,
Department of Computer Science, University of British Columbia, Vancouver,
British Columbia, 1992.
[Johnson87] Mark Johnson, Multivariate
Statistical Simulation, John Wiley & Sons, New York, New York,
1987.
[Koenderink90] Jan Koenderink, Solid
Shape, MIT Press, Cambridge, Massachusetts, 1990.
[Lyon93] Richard Lyon, "Phong Shading Reformulation
for Hardware Renderer Simplification", Apple Technical Report #43,
Apple Computer, Inc. 1993.
[Neyret95] Fabrice Neyret, "A General and Multiscale
Model for Volumetric Textures", Graphics Interface `95, 1995.
[Olano93] Marc Olano and Terry Yoo, "Precision
Normals (Beyond Phong)", Technical Report TR93-021, Department of
Computer Science, University of North Carolina, Chapel Hill, North Carolina,
1993.
[Perlin84] Ken Perlin, "Unified textural reflectance
model", Advanced Image Synthesis course notes, SIGGRAPH `84
(Minneapolis, Minnesota, July 23-27, 1984). ACM SIGGRAPH, New York, 1984.
[Poulin90] Pierre Poulin and Alain Fournier, "A
Model for Anisotropic Reflection", Proceedings of SIGGRAPH `85 (San Francisco,
California, July 22-26, 1985). In Computer Graphics, v19n3, ACM
SIGGRAPH, New York 1985.
[Ward92] Gregory Ward, "Measuring and Modeling
Anisotropic Reflection", Proceedings of SIGGRAPH `92 (Chicago, Illinois, July
26-31, 1992), In Computer Graphics, v26n2, ACM SIGGRAPH, New York,
1992.
[Westin92] Stephen Westin, James Arvo, Kenneth
Torrance, "Predicting Reflectance Functions from Complex Surfaces",
Proceedings of SIGGRAPH `92 (Chicago, Illinois, July 26-31, 1992), In
Computer Graphics, v26n2, ACM SIGGRAPH, New York, 1992.
[Williams83] Lance Williams, "Pyramidal
Parametrics", Proceedings of SIGGRAPH `83 (Detroit, Michigan, July 25-29,
1983). In Computer Graphics, v17n3, ACM SIGGRAPH, New York, 1983.








![n([x y]/z, u, S)](hemisphere.gif)
![n([x y]/(z+1), u, S)](sphere.gif)