Fractals

A fractal is a geometric object which can be divided into parts, each of which is similar to the original object.

• Trees and ferns are fractal in nature and can be naturally modeled on a computer using a recursive algorithm.
• This recursive nature is clear — take a branch from a tree or a frond from a fern and you will see it is a miniature replica of the whole: not identical, but similar in nature.
• Mathematicians and computer scientists are interested in how such fractal structures can be described.
• They have practical applications as well, such as generating realistic looking natural objects in computer graphics.

Koch snowflake

A Koch snowflake is a simple example.

It's the result of infinite additions of triangles to the perimeter of a starting triangle.

Each time new triangles are added (an iteration), the perimeter grows, and eventually approaches infinity.

In this way, the fractal encloses a finite area within an infinite perimeter.

Self similarity

A complex fractal shape emerges from the simple repetition of a basic shape at a smaller and smaller scale.

When you zoom in to a fractal, at every scale it appears the same.

If you "zoom in" on the infinite version of a Koch curve, you see more and more detail, but it all looks the same.

Here's an animation:

Nature seems fractal

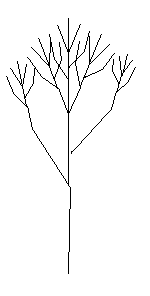
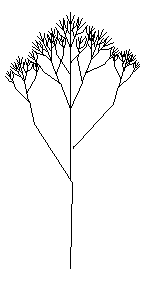
Self-similarity makes fractals useful for modeling natural systems.

Consider the shape of a tree. From the trunk of a tree shoot off several branches.

Each branch then repeats this branching pattern and gives rise to smaller branches.

So the tree branching is self-similar.

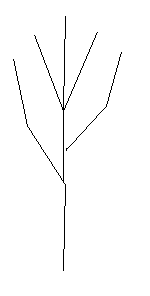some material adapted from MathBlues