Fibonacci numbers in nature
|
UMBC CMSC 201 Fall '05 CSEE | 201 | 201 F'05 | lectures | news | help |

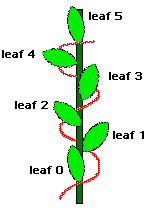
The arrangement of leaves or twigs on a stem (phyllotaxis, from the Greek word phyhllon meaning leaf and taxis meaning arrangement) correspond to Fibonacci numbers. Select one leaf as a starting point and count up the leaves on the stem until you reach a leaf directly above your starting point. The number of leaves is usually a Fibonacci number. In the above figure, starting from the bottom leaf, we count up 5 leaves to find the next one directly above the bottom leaf. Also, you can count the number of turns around the stem, as you go from a leaf to one directly above it. This too is usually a Fibonacci number. For a pussy willow, typical numbers are 13 for the number of "leaves" and 5 times around.
fib(n) = undefined for n<0 fib(0)=fib(1)=1 fib(n)=fib(n-1)+fib(n-2) for n>1
int Fib(int n) {
if (n < 2)
{
return(1);
}
else
{
return(Fib(n - 1) + Fib(n - 2));
}
}
int Fib(int n)
{
int i, f1=1, f2=1, temp;
if (n < 2)
{
return(1);
}
else
{
for(i = 2; i < n; i++)
{
temp = f1;
f1 = f2;
f2 = temp + f2;
}
return (f1 + f2);
}